Relative Raman Intensities in C₆H₆, C₆D₆, and C₆F₆: a Comparison of Different Computational Methods

Stephen D. Williams, Timothy J. Johnson*, Thomas P. Gibbons, and Christopher L. Kitchens

A. R. Smith Department of Chemistry, Appalachian State University, Boone, NC 28618

*Battelle Pacific Northwest National Laboratory, P.O. Box 999 Mailstop K8-88, Richland, WA 99352

Abstract: The accuracy of various computational methods (Hartree-Fock, MP2, CCSD, CAS-SCF, and several types of DFT) for predicting relative intensities in Raman spectra for C₆H₆, C₆D₆, and C₆F₆ were compared.  The predicted relative intensities for n₁ and n₂ were compared with measured relative intensities.  While none of these methods excelled at this prediction, Hartree-Fock with a large basis set was most successful for C₆H₆ and C₆D₆, while PW91PW91 was the most successful for C₆F₆.

Keywords: relative Raman intensity, ab inito, Hartree-Fock, MP2, DFT, CCSD, CAS-SCF

Introduction: The assignment of Raman spectra, even for small sized molecules, is not a simple task.  Quantum mechanically computed vibrational frequencies can provide significant help in this task, since the typical errors and empirical corrections for these frequencies are well known [1].  However, frequencies may not be enough to assign the spectrum, for example when a weak fundamental is near a combination or overtone.  Quantum mechanically computed Raman intensities are quite helpful in such cases, particularly if their reliabilities are known.  There have been several studies of computed Raman intensities compared to experiment; these have focused on one of a few methods or basis sets, and have not attempted to survey several different types of computation methods.  These studies include Hartree-Fock methods for ethylene [2], benzene [3], HFCs [4], and triptycene [5]; DFT methods for N₂, HF, and ethane [6], as well as water, ammonia, and methane [7]; and hybrid DFT methods for azulene [8], porphine [9], PAHs [10], and aniline and its radical cation [11].  While some of these (small molecule) studies compare the computed Raman intensities with measured absolute Raman activities or cross sections, most compare the computed intensity to an experimental Raman spectrum, and in most of these cases, the comparison is made to an intensity-uncorrected spectrum.  As McCreery [12] points out in his excellent review, not correcting for the spectrometer’s response can dramatically distort a Raman band’s intensity.  It is thus difficult to gauge the theoretical to experimental intensity comparisons of some of these reports.  Shinohara et al. [10] do make comparisons with corrected spectra, but they do not include the C-H stretching bands.

We have chosen to compare computed relative Raman intensities with accurately measured relative intensities, using several methods including Hartree-Fock, correlated ab initio (MP2, CCSD, CAS-SCF), pure DFT (PW91PW91), and hybrid DFT (B3LYP, B3PW91, BB1K).  In order to be as certain as possible that we were comparing intensities of correctly assigned modes, we considered the two a_1g modes of C₆H₆, C₆D₆, and C₆F₆.  These modes are n₁, the totally symmetric C-X stretching mode, and n₂, the totally symmetric ring C-C stretch; they are readily assigned due to their strongly polarized nature.  We assessed the quality of a computational method on how well it reproduces the experimental ratio of the relative intensities of these modes, I(n₁)/I(n₂), since determining absolute Raman cross sections is difficult, and our hope is to provide practical advice to those who routinely use Raman spectroscopy in their work. We also show a comparison of a theoretically simulated spectrum with the corresponding corrected experimental spectrum.

Experimental: Fourier transform Raman spectra were measured with an FT-Raman spectrometer using 1064 nm excitation and 2 cm^-1 resolution.  180° backscattered light was collected, typically averaging 512 interferograms.  Polarized spectra were also collected, typically measured with 4 cm^-1 resolution.  The spectra of the neat liquids were recorded using a Bruker FRA 106 Raman module coupled to the interferometer of a Bruker IFS 66v/S vacuum Fourier infrared spectrometer.  A similar FTIR spectrometer has been previously described [13], using the methods suggested by IUPAC [14]. The 106 Raman accessory consists of a CW 1.064 μm Nd:YAG laser with a focused or unfocused laser spot and with either 90^o or 180^o backscatter spectral light collection. 

As described by Simon et al. [15], a notch filter in the FRA 106 removes the Rayleigh scattered photons; the Raman-scattered light is modulated by the FTIR interferometer and focused onto a sensitive liquid-nitrogen cooled Ge detector [16].  In the present case the interferometer’s wavelengths are referenced to those of the HeNe laser.  These were calibrated in the near-IR by using a white light source and the 2 ← 0 overtone transition of ~22 Torr of neat carbon monoxide [17] in a 10 cm cell and adjusting the spectrometer’s measured wavelengths (via the HeNe frequency) to match those of the HITRAN database [18].    To calibrate the Raman Nd:YAG laser wavelength and thus the Raman scattered frequencies, a strong scatterer, elemental sulfur, was used and the laser wavelength empirically shifted such that the Stoke’s and anti-Stoke’s Raman shifts were equal to within 0.2 cm^-1 for a few of the strongest lines. 

Calibration of the scattering intensity as function of wavelength is somewhat more complicated.  The Raman module has a 3000 K white light source whose intensity is scattered into the spectrometer off a NIST-traceable Spectralon surface mounted at the sample position.  The instrument response function as a function of wavelength is then generated by ratioing this spectrum relative to the intensity predicted by Planck’s law for a 3000 K source.   Subsequent spectra are then multiplied by the (frequency dependant) scaling factor.  The quality of the intensity correction was assessed by measuring the intensities in the corrected Stokes and anti-Stokes spectra; the relative intensities were within a few percent of the expected value ([19], equation 4.36).  As McCreery has pointed out, [12] obtaining Raman intensity values that correlate even on a relative scale, i.e. that properly ratio out the instrumental response, is more challenging than first supposed.

For polarization experiments the natural polarization of the laser was used.  A reducing Jacquinot stop and a calcite Glan-Taylor analyzer (i.e. cross-polarizer) were placed after the Raman notch filter at the focal position of the interferometer’s collimator mirror.  Perpendicular and parallel orientations were obtained by rotating the analyzer to the 0^o and 90^o positions.  The method was verified by measuring the parallel and perpendicular spectra of CCl₄ whose depolarization ratio is known [20]. The depolarization ratios of natural isotope benzene, particularly the symmetric C-H stretching and ring breathing modes, have also been reported and were reproduced [20, 21].

Relative intensities of the two a_1g stretching modes (n₁, C-X stretch and n₂ , C-C stretch) were determined by fitting the appropriate bands to a pseudo-Voigt lineshape function [22]:

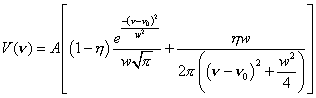                                                     (1)

In this four parameter function the peak area is A, the full width at half maximum is w, the peak center is n₀, and h is the fraction the Lorentzian contributes to the peak.  Sigmaplot was used for the curve fitting.  Ratios of the resulting areas were then compared to corresponding theoretical values for C₆H₆, C₆D₆, and C₆F₆.  We also measured the spectrum of ¹³C₆H₆ but did not include this in the analysis due the extensive Fermi resonance perturbation of the CH stretching modes [23].

The computations were carried out with Gaussian98 [24] on an Intel PC and Gaussian03 [25] on an SGI altix computer.  The default basis sets in Gaussian were used except for a few calculations with Truhlar’s MG3 [26] basis set.  For each calculation the molecular geometry was optimized followed by a frequency calculation.  The geometry was constrained to have D_6h symmetry during the optimization.  For C₆F₆ some MP2 constrained optimizations yielded structures with a single imaginary frequency associated with an out-of-plane motion of alternate C atoms.  This problem was only observed with large Pople basis sets (6-311+G(3df,2p)), and did not occur when Dunning correlation consistent basis sets [27] were used.   For the Hartree-Fock, DFT, and MP2 calculations described here the automatic methods in Gaussian were used to compute the Raman activities (keyword: freq=Raman), but for other calculations (CCSD and CAS-SCF) this automatic method was not available.  What appears in the Gaussian output as the Raman activity is (following the notation of Long [19]).  Here is the square magnitude of derivative of the isotropic part of the polarizability tensor with respect to the k^th normal mode, and likewise  for the anisotropic part of the polarizability, where the derivatives are evaluated at zero displacement.  (The factor of 7  is for 90° scattering; for 180° scattering a factor of 4 appears instead.)  For the CCSD and CAS calculations the normal modes (included in the Gaussian freq=hpmodes output) for the two a_1g modes were used to generate a series of molecular structures displaced along the mass weighted normal mode (using the reduced mass reported by Gaussian).  The polarizability tensor components were then computed for each of these and numerical differentiation was used to estimate the polarizability derivatives; these were then used to calculate the needed polarizability tensor invariants for the Raman activities, following standard methods [19].  This numerical method was also applied to a few Hartree-Fock calculations; the Raman activities derived from these point-by-point polarizability curves differed by at most a few percent from the automatic ones from the same calculation.

The CAS-SCF calculations used a (6,6) CAS where the active space included the 6 p MO’s composed primarily of the 2p_z C atom AO’s.  A series of single point calculations starting with STO-3g and gradually increasing to the largest basis set was used to ensure that the correct orbitals were used in the highest level CAS; visualization of these orbitals with GaussView confirmed this.

Results: There are two strong fundamental CH stretching modes in the Raman spectrum of benzene; these are usually denoted by n₁ and n₁₅ of a_1g and e_2g symmetry [28], although other notations are sometimes used [29].  These bands overlap in spectra of room temperature samples, to the extent that recent [29] absolute Raman scattering cross section measurements of benzene vapor have reported only the sum of the cross sections for these modes.  For our intensity measurements we need the contribution to the total intensity for n₁ only.  The pseudo-Voigt curve fitting procedure is successful in resolving these two contributions, as shown in Figure 1 below.
Figure 1

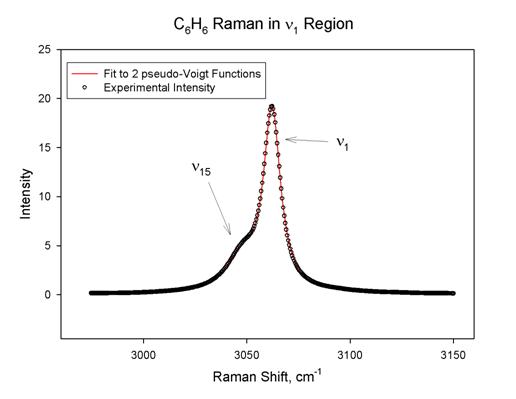
In this case the R² statistic was 0.9998 and the areas for n₁ and n₁₅ are 279±1 and 105±1, in arbitrary units.  The fits for the other modes and species were not always this good, but in all cases the R² statistic was at least 0.993.  A particularly challenging fit was for n₁ in C₆F₆.  This band is quite weak (weaker than some overtones in the spectrum) and is complicated by the presence of an isotopic band and a broad underlying peak.  The area was found to be 2.7±0.5 with R² = 0.998.  Note that the intensity for n₁ in C₆F₆ is about 1% of that for n₁ in C₆H₆.   The fit for this band is shown in Figure 2 below.
Figure 2

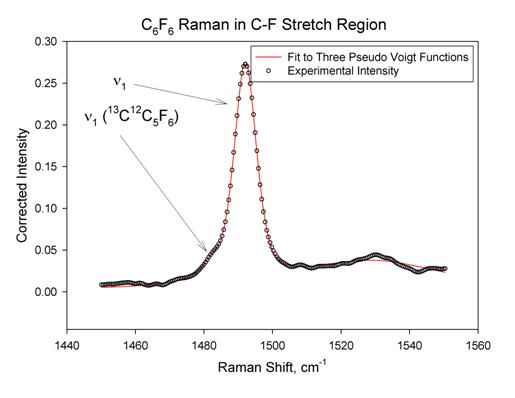
The intensity of n₁ in the C₆F₆ Raman spectrum is quite weak and is of similar intensity to an overtone band that is somewhat close in frequency.  Since both of these are totally symmetric, they have the same polarization properties, so polarization measurements did not help in confirming the assignment for n₁.  We confirmed the assignment of n₁ by noting that the nearby totally symmetric mode was at nearly exactly twice the frequency of a forbidden (b_2g) fundamental (n₇), and that the observed isotopic shift in frequency upon substitution of a single ¹³C atom was in near perfect agreement with the predicted isotopic shift for n₁ computed at the B3LYP/6-311+g(3df) and MP2/ccpVTZ levels of theory.  This isotopic band is not observed in the spectrum of C₆H₆; its appearance in the C₆F₆ spectrum is a consequence much larger atomic mass of fluorine compared to hydrogen.  Our assignment of the C₆F₆ Raman spectrum is shown in Figure 3 below, and agrees well with previous assignments [30].
Figure 3

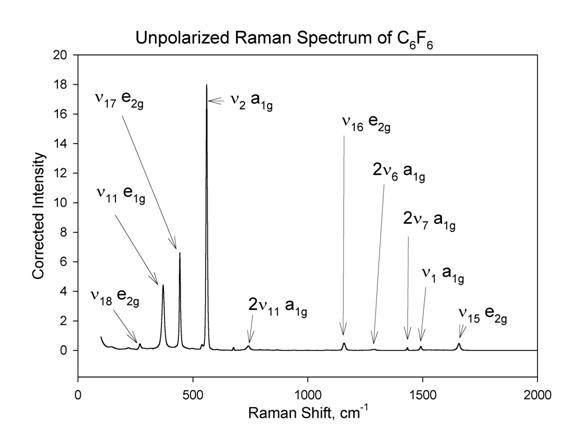
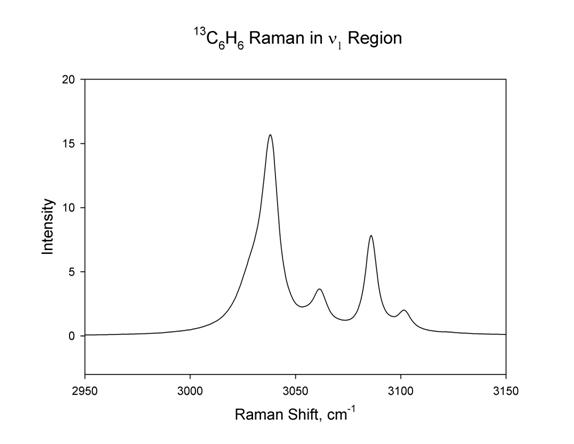
The Raman spectrum for ¹³C₆H₆ was planned for this study but it turned out not to be suitable for measuring intensities for n₁, due to Fermi resonance with overtones.  This resonance perturbs the intensities of the CH stretching modes in a way that is not simple to correct.  The Fermi resonance perturbed CH stretching region is much more complicated for ¹³C₆H₆ compared to C₆H₆ as shown in  Figure 4  below.
Figure 4

We considered C₆H₆ as a test case, since Ozkabak et al. [3] had good results with Raman intensities computed at the Hartree-Fock level for this compound.  Methods that seemed relatively poor for C₆H₆ were not used to predict intensities for C₆D₆ and C₆F₆.  We compared the experimental intensity ratio I(n₁)/I(n₂) (ratio of areas from the curve fitting) with the predicted intensity ratio from a given level of theory.  As mentioned previously, Gaussian does not predict the Raman intensity, rather it predicts the Raman activity.  As McCreery [12] has pointed out, the intensity of a Raman band has contributions from three sources: a part that is intrinsic to the scattering molecule (this is Gaussian’s Raman activity), a part that depends on temperature (which affects the population of the scattering vibrational state), and a part that is dependent on the exciting laser frequency and the type of photometric detection in the Raman spectrometer.  In the notation of Long [19], this intensity for 180° scattering, Stokes shift, and power detection, may be represented as [19, 3]:
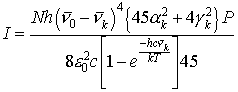                                                                         (2)
where N is the number of molecules excited by the laser, h is Planck’s constant, is the exciting laser wavenumber, is the wavenumber of the vibrational mode, c is the speed of light, k is Boltzmann’s constant, T is the temperature, e₀ is the permitivity of free space, P is the laser irradiance, is the squared derivative of the isotropic part of the polarizability tensor with respect to the k^th normal mode, evaluated at zero displacement, and  is the squared derivative of the anisotropic part of the polarizability tensor with respect to the k^th normal mode, evaluated at zero displacement.  This is the appropriate formula for our instrument.  Some common modifications might be: if a photon counting detector is used, the should be replaced with [12], and if 90° scattering is measured, the 4 should be replaced with a 7 [19].  Since we have restricted our study to the two a_1g stretching modes (since we can be very confident in their correct assignment), the  term is unimportant since it is zero for these totally symmetric vibrational modes; scattering geometry is not a factor for our study.  Hence for every method studied, we converted the computed Raman activity into a corresponding intensity appropriate to our experimental conditions, then calculated the I(n₁)/I(n₂) intensity ratio.

The results for this computed prediction of intensity ratio are presented in Table 1 below.
Table 1

Method	Basis Set	I(n1)/I(n2)
Experimental		0.91±0.01
RHF	6-311+g(3df,2p)	1.037
RHF	6-311++g(3df,2p)	1.038
RHF	6-31++g(d)	1.157
RHF	6-31+g(d)	1.166
MP2	aug-cc-pvdz	1.354
B3PW91	aug-cc-pvtz	1.442
CCSD	aug-cc-pvdz	1.447
B3LYP	6-311+g(3df,2p)	1.458
BB1K [31]	MG3 [26]	1.467
MP2	6-31+g(d)	1.522
B3LYP	6-31+g(d)	1.583
PW91PW91	aug-cc-pvtz	1.615
MP2	cc-pvtz	1.823
CAS(6,6) p	aug-cc-pvdz	2.193
CAS(6,6) p	6-31g	3.662

There are three trends worth noting for the results in Table 1.  One: for any given method, the results generally improve with larger basis sets, and the inclusion of diffuse functions is particularly important, as noted by Ozkabak [3].  Two: Hartree-Fock seems to be superior to methods that include in various ways the electron correlation energy.  Three: all of the methods tested overestimate the intensity of the C-H stretching mode compared to the C-C stretching mode.  It is also clear from Table 1 that there is no benefit for predicting Raman intensities from treating the basis functions that contribute to the 6 p MOs in a completely equivalent fashion as was done in the CAS(6,6) calculations.

Most of the methods in Table 1 were also applied to C₆D₆ and C₆F₆, except for the CAS(6,6) calculations (since they were quite poor for C₆H₆), and the CCSD calculations since they were too expensive for C₆F₆.  The results for these methods on two other species are shown in Table 2 below.
Table 2

Method	Basis set	I(n1)/I(n2) C6D6	I(n1)/I(n2) C6F6
Experimental		0.646±0.004	0.0178±0.0003
RHF	6-311+g(3df,2p)	0.662	0.140
RHF	6-31+g(d)	0.776	0.134
MP2	aug-cc-pvdz	0.860	0.073
PW91PW91	aug-cc-pvtz	0.908	0.0317
B3PW91	aug-cc-pvtz	0.908	0.0604
B3LYP	6-311+g(3df,2p)	0.92	0.0650
BB1K [31]	MG3 [26]	0.943	0.106
MP2	6-31+g(d)	0.984	0.0891
B3LYP	6-31+g(d)	1.021	0.0660
MP2	cc-pvtz	1.182	0.0850

The results in Table 2 show that, like the case of C₆H₆, all of the methods tested overestimate the C-X stretching intensity compared to the C-C stretching intensity.  They also suggest that Hatree-Fock with a large basis set is successful for C₆D₆, as it was for C₆H₆, but that it is quite poor for C₆F₆.  Table 2 also makes it clear that none of these methods is very good for C₆F₆.  It seems that accurate prediction of the intensity of both the most intense, and one of the least intense bands in the Raman spectrum is quite challenging.  The PW91PW91/aug-cc-pvtz calculations are much better than the others, overestimating the C-F stretching intensity by only 80% compared to the C-C stretching intensity; although rather poor for C₆H₆, this method did rather well on C₆D₆ also.

Discussion: It is quite unexpected that the Hartree-Fock methods seem to be superior to methods that include the electron correlation energy for predicting Raman intensity in C₆H₆.  It seems likely that this unexpected result is due to a fortuitous cancellation of errors.  It is possible that this cancellation involves the anharmonic nature of the C-H stretching modes.  Since the automatic Raman activities in Gaussian are computed on the assumption of harmonic vibrations, and the derivation of equation 2 is also based on the assumption of both electrical and mechanical harmonicity, it may be that neglecting anharmonicity may cancel some of the error in neglecting electron correlation energy.  Indeed, Maslen et al. [32] have shown that at the Hartree-Fock level, anharmonic corrections to Raman intensity are quite small, but they make no claim that this will be the case for correlated methods.  We are investigating methods to develop an intensity formula like equation 2 that does not depend on the assumption of mechanical harmonicity.

With the methods described here, it is possible to simulate the entire Raman spectrum from the activities computed by Gaussian.  Equation 2 may be used to convert these activities into the corresponding intensities predicted for a given sample temperature, laser frequency, and type of detector.  A simple way to do this is to assume that all of the Raman band will be described by Lorentzian peaks with a common width, whose areas are proportional to the predicted intensity.  Figure 5 below shows such a simulation for the complete Raman spectrum of C₆D₆, using the results from a calculation at the RHF/6-311+g(3df,2p) level of theory.
Figure 5

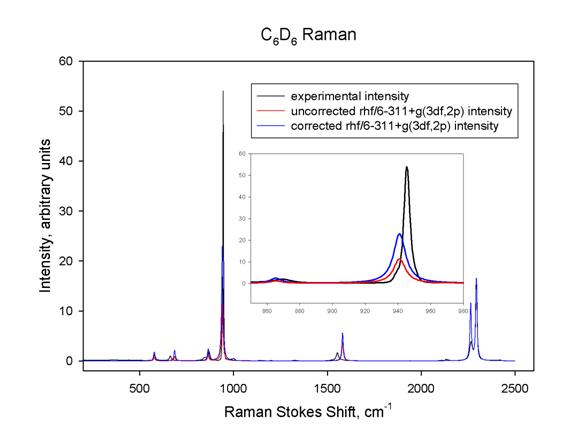
In this figure all of the predicted frequencies were scaled so that the predicted and observed n₁ frequencies would match; the predicted intensities were scaled so that the n₁ intensities would match; then a common peak width for all of the Lorentzians was chosen so that the n₁ lineshapes would match as closely as possible.  The black curve is the experimental intensity, corrected for spectrometer response; the blue curve is the predicted Raman intensity; and the red curve is the predicted Raman activity, uncorrected for laser frequency, temperature, and type of detector.  The inset clearly shows that such correction is quite important; the area under the blue curve is nearly equal to that under the black curve, but they have different peak widths.  The red curve has significantly smaller area.

Conclusions: For predicting the Raman intensities for hydrocarbons we recommend the use of Hartree-Fock calculations with a large basis set including diffuse functions.  For other types of molecules, or where CH stretching intensity is not of interest, perhaps a DFT method such as PW91PW91 with a basis set including diffuse functions would be better.  This latter choice has the advantage that it will also produce more accurate vibrational frequencies than will the Hartree-Fock calculations.

Acknowledgements: A portion of the research described in this manuscript was performed at the W.R. Wiley Environmental Molecular Sciences Laboratory, a national scientific user facility sponsored by the U.S. Department of Energy’s Office of Biological and Environmental Research and located at the Pacific Northwest National Laboratory.  PNNL is operated for the Department of Energy by Battelle.  Computer time was supported by collaborative hpc resources funded through the University of North Carolina Office of the President.

References:

1. Scott, A. P.; Radom, L. J. Phys. Chem. 1996, 100, 16502, http://srdata.nist.gov/cccbdb/vsf.asp (accessed 8/13/2004).
2. Kormornicki, A., McIver, J. W. J. Chem. Phys. 1979, 70, 2014.
3. Ozkabak, A. G.; Thakur, S. N., Goodman, L. Int. J. Quantum Chem. 1991, 39, 411.
4. Tai, S.; Papasavva, S.; Kenny, J. E.; Gilbert, B. D.; Janni, J. A.; Steinfeld, J. I.; Taylor, J. D.; Weinstein, R. D. Spectrochim. Acta, Part A, 1999, 55, 9.
5. Furlan, A.; Fischer, T.; Fluekiger, P.; Güdel, H. U.; Leutwyler, S.; Lüthi, H. P.; Riley, M. J.; Weber, J. J. Phys. Chem. 1992, 96, 10713.
6. Johnson, B. G.; Florian, J. Chem. Phys. Lett. 1995, 247, 120.
7. Stirling, A.; J. Chem. Phys. 1996, 104, 1254.
8. Kozlowski, P. M.; Rauhut, G.; Pulay, P. J. Chem. Phys. 1995, 103, 5650.
9. Kozlowski, P. M.; Jarzecki, A. A.; Pulay, P.; Li, X. Y.; Zgierski, M. Z. J. Phys. Chem. 1996, 100, 13985.
10. Shinohara, H.; Yamakita, Y.; Ohno, K. J. Mol. Struct. 1998, 442, 221.
11. Wojciechowski, P. M.; Zierkiewicz, W.; Michalska, D.; Hobza, P. J. Chem. Phys. 2003, 118, 10900.
12. McCreery, R. L. Photometric Standards for Raman Spectroscopy in Handbook of Vibrational Spectroscopy, Chalmers, J. M. and Griffiths, P. R., Eds.; Wiley, New York, 2002.
13. T.J. Johnson, R.L. Sams, T.A. Blake, S.W. Sharpe and P.M. Chu, “Removing Aperture-Induced Artifacts from FTIR Intensity Values,” Appl. Opt. 41, (2002), 2831-2839. 
14. J. E. Bertie, “Specification of Components, Methods and Parameters in Fourier Transform Spectroscopy by Michelson and Related Interferometers”, Pure and Appl. Chem. 70(10), (1998), 2039-2045. 
15. B. Schrader, A. Hoffmann, A. Simon, R. Podschadlowski and M. Tischer, “NIR FT-Raman-Spectroscopy, State of the Art,” J. Molecular Struct. 217, (1990), 207-220.
16. D.B. Chase, “Fourier Transform Raman Spectroscopy,”  J. Am. Chem. Soc. 108, (1986), 7485-7488.
17. S.W. Sharpe, T.J. Johnson, R.L. Sams, P.M. Chu, G.C. Rhoderick and P.A. Johnson, “Gas-phase Databases for Quantitative Infrared Spectroscopy,” Applied Spectroscopy, 58(12), (2004), 1452-1461.  
18. L.S. Rothman, et al., “The HITRAN Molecular Spectroscopic Database: Edition of 2000 Including Updates through 2001,” J. Quant. Spectrosc. Radi. Transf., 82, (2003), 5-44.
19. Long, D. A. Raman Spectroscopy, McGraw-Hill: New York, 1977, equations 3.18, 3.80 and 4.34.
20. A. Hoffmann, S. Keller, B. Schrader, R. Ferwerda and J. H. van der Maas,  “Polarization Measurements in Near-Infrared-Fourier Transform Spectroscopy,  J. Raman Spectr. 22(9), (1991), 497-503.
21. B. Schrader A. Hoffmann, A. Simon, and J. Sawatzki, “Can a Raman Renaissance be Expected via the Near-infrared Fourier Transform Technique?” Vibrational Spec. 1, (1991), 239-250.
22. Angel, R. J., J. Appl. Cryst. 2003, 36, 295-300.
23. Fernandez-Sanchez, J. M.; Murphy, W. F. Chem. Phys. 1994, 179, 479.
24. Gaussian 98, Revision A.9, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria,  M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr.,  R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam,  A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi,  V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo,  S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui,  K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari,  J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul,  B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi,  R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham,  C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill,  B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez,  M. Head-Gordon, E. S. Replogle, and J. A. Pople,  Gaussian, Inc., Pittsburgh PA, 1998.
25. Gaussian 03, Revision B.04, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria,  M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven,  K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi,  V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega,  G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota,  R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao,  H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross,  C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev,  A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala,  K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg,  V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain,  O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari,  J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford,  J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz,  I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham,  C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill,  B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople,  Gaussian, Inc., Pittsburgh PA, 2003.
26. Fast, P. L.; Sanchez, M. L.; Truhlar, D. G.; Chem. Phys. Lett. 1999, 306, 407; Curtiss, L. A.; Redfern, P. C.; Raghavachari, K.; Rasslov, V.; Pople, J. A.; J. Chem. Phys. 1999, 110, 4703; Curtiss, L. A.; Raghavachari, K.; Redfern, P. C.;  Rasslov, V.; Pople, J. A.; J. Chem. Phys. 1998, 119, 7764.
27. Kendall, R. A.; Dunning, T. H. Jr.; Harrison, R. J.; J. Chem. Phys. 1992, 96, 6796.
28. Herzberg, G. Molecular Spectra and Molecular Structure II. Infrared and Raman Spectra of Polyatomic Molecules, Van Nostrand Reinhold: New York, 1945.
29. Fernandez-Sanchez, J. M.; Montero, S.; J. Chem. Phys. 1989, 90, 2909-2914.
30. Delbouille, L.; J. Chem. Phys. 1956, 25, 182; Laposa, J. D.; Montgomery, C.; Spectrochim. Acta. 1982, 38A, 1109; Yumura, T.; Koga, M.; Hoshikawa, H.; Nibu, Y.; Shimada, R.; Shimada, H.; Bull. Chem. Soc. Jpn. 1998, 71, 349; Suzuki, Y.; Shimada, H.; Shimada, R. Bull. Chem. Soc. Jpn. 1996, 69, 3081.
31. Zhao, Y.; Lynch, B. J.; Truhlar, D. G.; J. Phys. Chem. 2004, 108, 2715-2719.
32. Maslen, P. E.; Handy, N. C.; Amos, R. D.; Jayatilaka, D.; J. Chem. Phys. 1992, 97, 4233-4254.